백준 2579 자바

백준 2579 동적 계획법

문제

문제는 위에 링크와 같다.

• 설명
  • 문제를 간단하게 설명하면 각 계단이 있는데 그 계단에 값이 있고 연속해서 계단을 3번을 건널 수 없고 최대값을 구하는 문제이다.

    

    DP[N]을 N개의 계단을 오르기 규칙에 의해 얻은 최대 점수라고 가정하자. N번째 계단은 무조건 밟아야 하기 때문에 N번째 계단이 1번 연속인 경우! N번째 계단이 2번연속인 경우! 이 2가지 경우를 나누어서 생각해 보자. 이제 중요한 3번째 계단이다.
    • (첫번째 경우) N번째 계단이 1번 연속인 경우 N-1번째 계단은 필요 없고, N-2번째 계단의 총점을 합쳐야 합니다.
      • DP[N] = DP[N-2] + A[N]
    • (두 번째 경우) N번째 계단이 2번 연속인 경우 N-1번째 계단은 밟아야 하고, N-2번째 계단은 무조건 밟으면 안되며, N-3번째 계단은 무조건 밟아야 하기 때문에 N-3번째 계단까지 얻은 점수를 더해주면 됩니다.
      • DP[N] = A[N] + A [N-1] + dp[N-3]
    • 코드는 이렇게 된다.package twoweekpractice;
      ​
      import java.io.BufferedReader;
      import java.io.IOException;
      import java.io.InputStreamReader;
      import java.net.Inet4Address;
      //점화식...
      public class Q2579 {
         public static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
         public static int stairs;
         public static int[] stairBox;
      ​
         public static void main(String[] args) throws IOException {
             stairs = Integer.parseInt(br.readLine());
             stairBox = new int[stairs + 1]; //계단 배열 초기화
      ​
             //각 계단 값 초기화
             for (int i=1; i<stairs + 1; i++) {
                 stairBox[i] = Integer.parseInt(br.readLine());
            }
      ​
             int[] dp = new int[stairs + 1];
             dp[1] = stairBox[1];
             if (stairs >=2 )
                 dp[2] = stairBox[1] + stairBox[2];
      ​
             for (int i=3; i<=stairs; i++) {
                 dp[i] = Math.max(dp[i-2]+stairBox[i],dp[i-3]+stairBox[i-1]+stairBox[i]);
            }
             System.out.println(dp[6]);
        }
      }
      ​
    한 줄평
    • 근데 아직 점화식을 처음에 생각하는게 쉽지가 않다..ㅠㅠㅠ

  • ---

  • 첫번째 계단을 밟았을 때는 그냥 첫 번째 계단의 값을 dp배열에 넣으면 된다. 두 번째 계단을 밟았을 때는 첫 번째 계단과 두 번째 계단을 더해서 dp배열에 넣어줘야한다.
  • 이런식으로 가지치기를 하면서 한껏 상상의 나래를 펼치고 있었다. 하지만 계속해서 수렁으로 빠지고 있었다. 그래서 동적계획법을 다시 읽어보고 점화식을 찾아내려고 하였다. 동적 계획법을 할 때 메모리제이션 을 활용해야 했다.
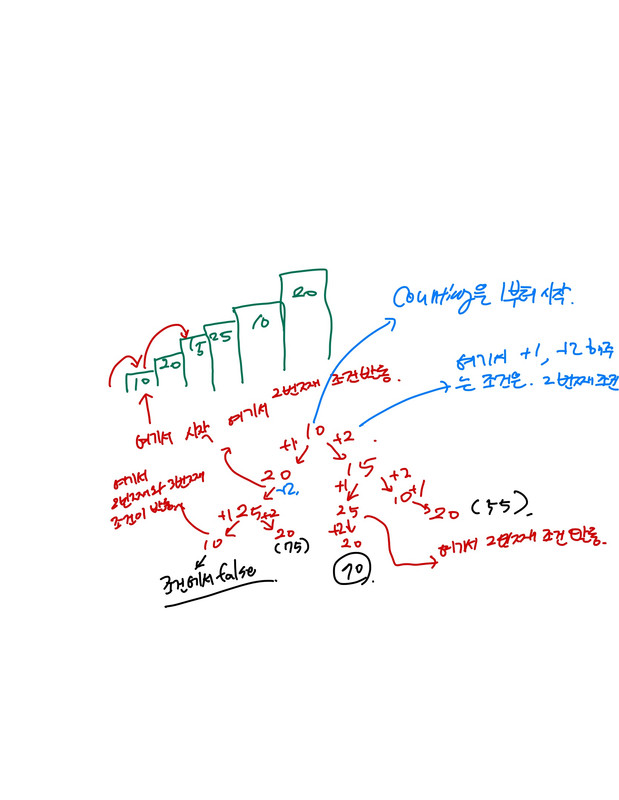
  • 처음에는 이걸 DFS로 풀려고 했다.. 갑자기 조금 챙피해지네요...😫 나의 생각은 밑에 그림과 같다.